Site officiel : GeoGebra.

GeoGebra est un logiciel très convivial qui permet de faire beaucoup de choses. Trop ? Personnellement, je n’aime pas trop les derniers développements qui font que ce logiciel «s’usinagazifie» à chaque mouture. Après le tableur très spécifique, un module de calcul symbolique est apparu sur les versions 4.2, remplacé par le moteur de Xcas (Giac) en version 4.4 (mais je préfère largement Xcas, plus fonctionnel), et géométrie 3D sur la version 5.

Le problème est que ce programme commence à très mal tourner sur des configurations anciennes ou pas trop puissantes, et la géométrie 3D est encore plus limitative. Et détail agaçant, depuis un certain temps, l’aide est uniquement en ligne, et plus en local sur votre ordi : il faut une connexion pour en bénéficier…

Je l’utilise sur ses fonctions de base : algèbre et géométrie, et j’oublie le reste. Sur ce terrain, il reste et de loin le plus intuitif et simple à utiliser (il y a beaucoup de concurrence, mais… bof !)

On peut faire quoi avec GeoGebra ?

1. •tracer des figures géométriques : points, droites, segments, cercles, parallèles, perpendiculaires, tangentes…
   

2. •le module de géométrie 3D est très utile en TS pour visualiser les problèmes
   

3. •bien entendu, quand on déplace un des composants de la figure, tout le reste suit : idéal pour conjecturer des résultats, et montrer une figure dans plusieurs configurations.
   

4. •définir et tracer des fonctions d’une variable x ; en prime, on peut avoir la dérivée et une primitive (embryon de calcul symbolique).
   

5. •il y a une foultitude de fonctions de calculs diverses, certaines très utiles, d’autres marginales.
   

6. •la qualité des graphismes est excellente, tant à l’écran qu’à l’imprimante. On peut bien entendu exporter ces graphiques pour illustrer des cours de manière extrêmement propre.
   

Et avec tout ça, que fait-on avec des élèves ?

1. •on peut construire des figures (dès le collège) et les déformer pour vérifier des conjectures.
   

2. •le protocole de construction n’est pas forcément simple : il faut savoir l’organiser de manière à ce que la figure soit déformable sans perdre ses propriétés fondamentales. Ex : tracer un parallélogramme qui le reste quand on déplace un de ses points. C’est largement aussi complexe et formateur que de tracer une figure sur papier à la règle et au compas. D’ailleurs, il faut souvent utiliser les techniques «traditionnelles» de construction : on a la même démarche qu’à la main, mais au final, on obtient une figure propre et qui peut évoluer facilement (c’est l’aspect géométrie dynamique).
   

3. •au lycée, on peut tracer des courbes de fonctions, calculer des dérivées (si on a rentré f(x), on tape juste f’(x) et on obtient la courbe de la dérivée et sa formulation algébrique). C’est plus confortable que l’écran de la calculette, et le zoom est très pratique à utiliser.
   

4. •on peut créer des paramètres modélisés par des curseurs à l’écran, et utiliser ces paramètres dans les fonctions ou constructions géométriques : idéal pour voir l’impact d’un paramètre sur une courbe ou une figure, il suffit de déplacer le curseur pour modifier le paramètre en continu.
   

5. •et bien entendu, j’ai quelques constructions toutes faites qui me servent à expliquer des notions fondamentales aux élèves : voir ci-dessous quelques exemples à télécharger.
   Mais attention ! Dans ce cas, le plus simple est le mieux. Vous pourrez constater que mes fichiers sont d’une simplicité technique déconcertante, car c’est ce qui se révèle le plus efficace du point de vue compréhension des notions par les élèves. Nous sommes très loin de la débauche de technicité de certains exemples qu’on trouve sur le net (et qui justifient toujours plus de fonctionnalités, et… d’obésité du logiciel) !

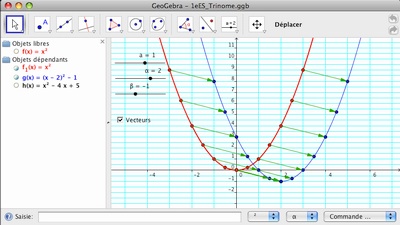
Trinôme du second degré

Les fonctions associées par translation ont été retirées du programme de 1e ES. C’était un concept mal aimé des élèves, mais je le conserve pour introduire ce trinôme.
La courbe représentative d’un trinôme du 2nd degré quelconque est une translation de la courbe des fonctions f(x)=ax^2.
Les coordonnées du vecteur de la translation donnent directement les coordonnées du sommet de la parabole, et surtout, la forme canonique du trinôme, qui ne tombe plus du ciel.
Et on parle de famille de courbes : des formulations algébriques différentes pour un même objet géométrique.

La dérivée

J’ai deux outils pour montrer de manière dynamique ce qu’est la dérivée :

1. •un outil très simple qui part d’une sécante à la courbe Cf, et dont on rapproche les deux points d’intersection pour se rapprocher de la tangente. L’unique aspect technique est caché, c’est une variation un peu sophistiquée de la valeur du curseur pour rendre celui-ci plus maniable. On peut afficher/masquer la tangente d’un clic.
   

2. •l’autre outil est assez complexe. J’en étais fier, mais en fait, il passe assez mal ! C’est à réserver aux élèves qui comprennent facilement les choses…
   On définit une fonction f (ici un polynôme d’ordre 3), on trace sa courbe Cf, le point A se déplace sur cette courbe, et pour toute position de A, on visualise la tangente à Cf et son coefficient directeur.
   On trace alors le point B, d’abscisse celle de A, et d’ordonnée le coefficient directeur de la tangente. Si on déplace A, on trace point par point la courbe de la fonction dérivée.
   Il faut activer la trace du point B et masquer la courbe de la dérivée f’ pour ce faire.
   Ca m’a permis de faire passer la notion de fonction dérivée chez certains élèves…
   

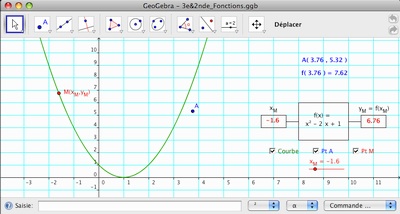
Courbe d’une fonction

Je vais peut-être étonner beaucoup de monde, mais la notion de courbe d’une fonction, dont la définition tient 1/2 ligne dans les cours de seconde et n’est souvent accompagnée d’aucun commentaire, est très mal comprise par beaucoup d’élèves !

Cet outil comprend une «machine de calcul» qui transforme un nombre à l’aide d’une formule quelconque (ici, un trinôme du 2nd degré, mais peu importe). Le couple de valeurs x et y mis ainsi en correspondance va engendrer un point M de coordonnées M(x, y). On transforme une paire de valeurs liées par un calcul algébrique en un objet géométrique, destiné à visualiser cette paire de nombres. Et en faisant varier x (curseur), on trace la courbe (qu’on a escamotée au préalable avec la case à cocher) point par point.

Il y a aussi le problème de l’appartenance d’un point à une courbe : c’est le point A, dont on affiche les coordonnées, et aussi le calcul de l’image de l’abscisse de A par f. Le point est sur la courbe quand cette image est égale à l’ordonnée de A.

Le cercle trigonométrique

Il s’agit du grand classique de l’enroulement de la droite des réels sur le cercle pour expliquer la notion de mesure d’angle en radian.

Techniquement, le souci est qu’après 1/2 tour, le point qui sert d’origine sur la droite sort de l’écran…

Accessoirement, on peut visualiser les coordonnées du point A, qui sont le cos et le sin de l’angle.